�v���O�����@�@�i2023�N8��26���j
���V���|�W�E��
10:00�`12:30 ��501����>�@�����i��@����u�i�ߌ���w�j
|
���u�� |
||
| 1 |
IB���w����̊T�v�A��ʐ��w�����IB���w����̈Ⴂ�̊T�v�A���w�̉��p��ƃe�N�m���W�[�̗��p �L�c�����i�Ƃ悾��܁j�AJill Ann Catingan�@�i�O�Y�w�������w�Z�j |
10:10�`10:50 |
| 2 |
���w�̎��ƂɃf�[�^���W���������Ӌ` ���c�^�i�������w�ْ��w�E�����w�Z�j |
10:50�`11:10 |
| �@ |
���x�e�� |
�@ |
| 3 |
�e�N�m���W�[��T���Ɏg�� ���q���j�i���ȗ��ȑ�w�j |
11:10�`11:40 |
| 4 |
�f�[�^�T�C�G���X�ɂ����鐔�w ���V�[�I�iNaoco Inc./T3Japan Administrator�j |
11:40�`12:00 |
|
���p�l���f�B�X�J�b�V���� |
||
| �@ | ��ꂩ��̎���A���ӌ������Ƃɓ��_��i�߂܂��B | 12:00�`12:30 |
��Workshop
| �@ |
A(504�����j |
B�i507�����j |
| 13:30�`14:20 |
���c�^�i�������w�ْ��w�E�����w�Z�j ���w�Z�uC ���v�̈�ɂ�����f�[�^���W�������ꂽ���Ƃ̌��� �����Z���T�[��p���ĕ����Ȃ���O���t��`�����Ƃ̎��H���ʓ����Љ��B�ߋ���T^3�N��ł������Z���T�[��p�������Ǝ��H����͐������Љ��Ă���B���߂ĉߋ��̔��\���e�ɖڂ�ʂ��ƁA�a�V�Ȏw���ł��邱�ƂɋC�Â������B���̈���ŁA�v���@��̌Â��������Ă��܂��B�w�����ׂ����e�͕ς��Ȃ����A���̂��߂Ɏg�p����@��ނ͂����Ԃ�V�����Ȃ��Ă����ۂ���B�R���i�Ђł�������Workshop�⌤�C��J���Ȃ������Ԃ��e�N�m���W�[�̐i���͎~�܂邱�Ƃ͂Ȃ������悤���B������A�w�����鋳�����V���ȋ@��Ŏ��Ǝ��H���邱�ƂɂȂ낤�B�V�����@��Ŏ��H����͂��߂̈���ɁA����̔N��𗧂��Ă���邱�Ƃ��肤�B |
�L�c�����i�O�Y�w�������w�Z�j �P������ѕ����Ɋւ���� GDC(Finance solver) ���������Ă���C���ۂ̖���TI-Nspire CXll���g���ĊF����ƈꏏ�ɉ����Ă����܂��B �@ Jill Ann Catingan�i�O�Y�w�������w�Z�j Statistics���v�Ɋւ����@(Chi square test�J�C2�挟��) ���������Ă���C���ۂ̖���TI-Nspire CXll���g���ĊF����ƈꏏ�ɉ����Ă����܂��B �@ �@ |
| 14:30�`15:10 |
�㏰�F���i���Q��w���������w�Z.�j �����Z���T�[����Z���T�[�𗘗p�������ȉ��f���Ƃ̌��� ���������p�o�̒P�U��q�^���������Z���T�[�Ōv�����A���̃f�[�^�𐔊w�T�u�Q�����v�ƘA�������Ď��H�������ƕ��s���܂��B�܂��A���Ǝ��H�͂ł��Ă��܂��A���N�x��萔�w���œ������Ă���Graphical Analysis Pro�̎g�p�ƍ���̌v�擙�����܂��B�R���i�Ђɂ��S���̍��Z�ł�Wi-Fi���������i���߁A���Z���w�u�f�[�^�̕��́v�u���v�I�Ȑ����v�����ۑ茤�����Ŋ��p�������܂��Graphical Analysis Pro�B�\�Ȃ�ΊF����ƈꏏ�Ƀf�[�^���W���Ȃ���ӌ����������{�������ƍl���Ă��܂��B �@ |
���q���j�i�������ȑ�w�j �}�`�̈�̒T������ �u���w���Ƃ�ICT�𗘗p���������v�ɂ��ďЉ��B�ۑ��u��ABC����ECD�͐��O�p�`�ł��BAD��BE���ؖ�����B�v�܂��C�ۑ�̍쐬�ɗ��ӓ_������B����͓��������Ƃ��Ɍ��₷����������悤�ɔz�����邱�ƁB���ɁA�ۑ�͎O�p�`�̍����𗘗p������̂����A�ɒ[�ȏꍇ���l���Ă�AD��BE�͓������Ȃ邱�Ƃ�������B��������O�p�`�̍������g���q���g��������B�ۑ�������Ƃɂ��A�����ɂ͉����ł���킯�ł͂Ȃ����A�ؖ��ł͐}�`�̈ʒu�W�ɂ��Ȃ��œ����悤�ɍ����������g�����Ƃ��ł���悳�ɐG��邱�Ƃ��ł���B |
| 15:20�`16:00 |
���V�[�I�iT3Japan�CNaoco Inc.�j �N���X�W�v�A�K���x�̌���A�Ɨ����̌��� ��L�̂Q�̌���́A�u�J�C��敪�z�v��p���Č��肵�܂����A�����ł͂��̐��w�I�Ȑ����͏Ȃ��܂��B�܂��s����g���ăJ�C���l�����߂܂����A������d��̋@�\���g���܂��B �E�����ɂ���ē���ꂽ�N���X�W�v�\������ꍇ�C�����x�����������̕��z�ɓK���i��v�j���邩�ǂ��������肷�邱�Ƃ��u�K���x�̌���v�Ƃ����܂��B�P�̃T�C�R����120��U���ē�����f�[�^����C���̃T�C�R���̕i���ɖ��Ȃ��ƌ����邩���l���܂��B �E2�ȏ�̕��ފ�����N���X�W�v�\�ɂ����āC���ފ�ԂɊ֘A�����邩�ǂ��������肷�邱�Ƃ��u�Ɨ����̌���v�Ƃ����܂��B�j���̍D���ȃA���R�[�������Ɋւ��鎿�⌋�ʂ���C�j���ƃA���R�[�������̍D�݂Ɋ֘A�����邩�ǂ������l���܂��B �@ |
���q���j�i�������ȑ�w�j ���̈�̒T������ �u���w���Ƃ�ICT�𗘗p���������v�ɂ��ďЉ��B�ۑ��ICT�\�t�g�Ŏ��o�����A��������s���낵�Ȃ��瓮�����A�������王�o�I��@����������_���I(���w�I)��@���v�l�����肵�ĉۑ�������߂����B�������̉ۑ��̈�u���������l���Ƃ��ē����Ƃ��A��������2tx�{t�Q�̒ʂ蓾��̈��}�����A���̎������߁B�v�ł́A�ۑ�̎���ICT�\�t�g�ɓ��͂��A�u���s����v���ăp�����[�^�����Ă݂�ƁA�O�Ղ����o������(��������)�����ɉ�������邱�ƂɂȂ�B�ۑ���������Ă��������̓T�^�ł���B�u���s����v���邽�߂ɂ́A�ۑ�𐳊m�ɗ������邱�Ƃɂ���B�����������ł��邪�A���k�͈ӊO�Ɖۑ肪���ł���̂���[���ǂݎ���ĂȂ����Ƃ�����B���ɁA�p�����[�^������\���Ă���̂��𗝉����钆����A����𐔎��ŕ\����Ή����Ɏ���B�w�K�̃|�C���g�ɂȂ�_���I��(���w�I��)��@�́A���܂ł̊w�K�E�m���␔���ό`�Ȃǂ̐��w�I�ȋZ�p�E�Z�\�Ȃǂ�p���邱�Ƃʼn������邱�Ƃ��ł���B |
�@
�@
�@
���@���
�@
�P���ْn��K�ɂ����q�������ׂɂ������������Z���C�G���x�[�^�łT��܂ł����ł��������B
�@
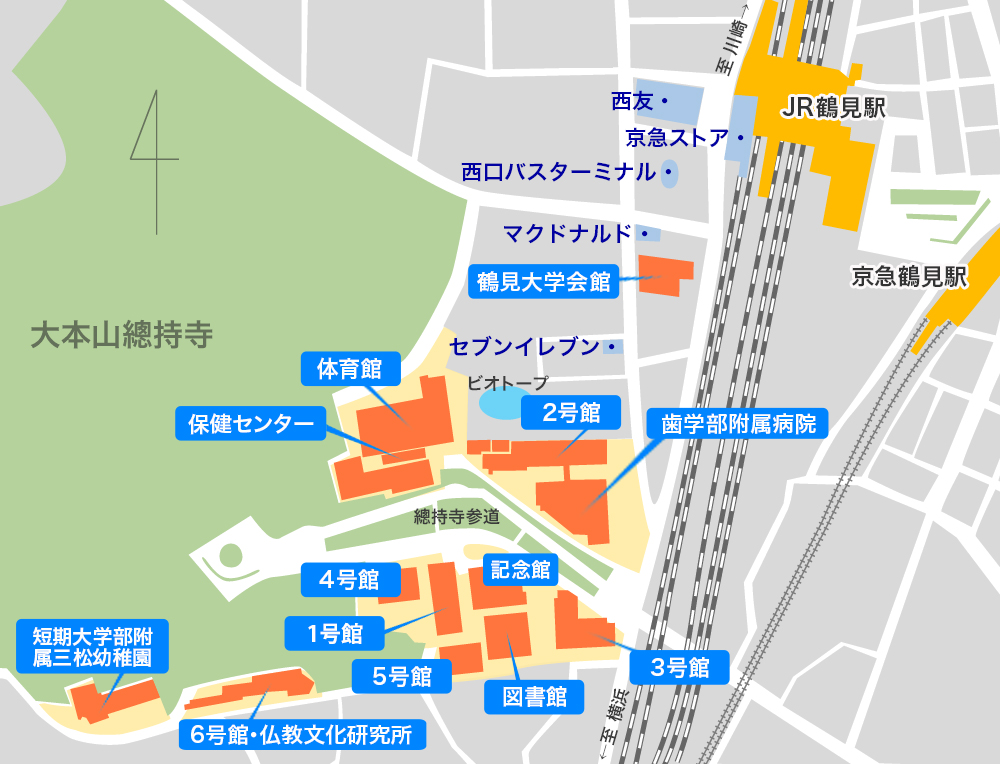
�@
�ߌ��w�������ԓk���T���@�@�@���}�ߌ��w���ԓk���V��
�@
�@
�@